Visualizing imaginary roots
The main post where all my quadratic posts are listed can be found here.
This is a redo of a post from 27 July 2012. It was lost in the great blog destruction of 2024, but resurrected here.
Learners have a difficult time with quadratics. Afterall, there can be 2 solutions, 1 solution, or no solutions in Algebra 1, and then in Algebra 2, we come at them with the fact that those equations with no solution really do have 2 solutions after all, they are just “imaginary” (could there be a worse name for them, really? Thanks a lot Descartes.”)
But I came across a picture on some site one day, and it has stuck with me. I never bookmarked it, or wrote down the site, so it is lost to me (and I have searched hard for it) but the work blew my mind, and as I have shown it to learners, they have at least gotten a sense that the “imaginary” really does have meaning. I will reconstruct that reasoning I saw here, and then prove it below.
Let’s begin with 2 equations and graphs that are simple, straight-forward and make sense.
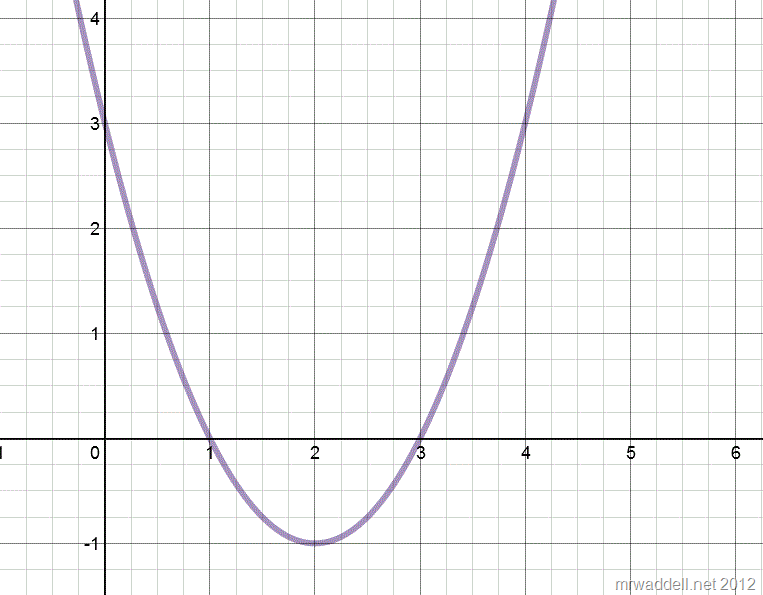
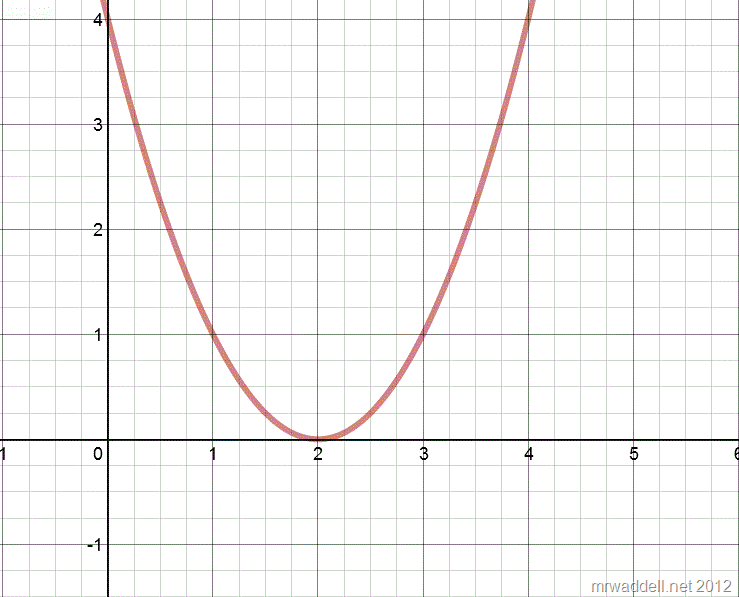
Respectively, the equations are: \[ y=x^2-4x+3 \quad \textrm{and} \quad y=x^2 - 4x +4 \]
A simple change of one number changes the number of solutions from 2 distinct to 2 repeating solutions, and learners don’t have a problem with that idea, generally. Then comes this trouble maker.
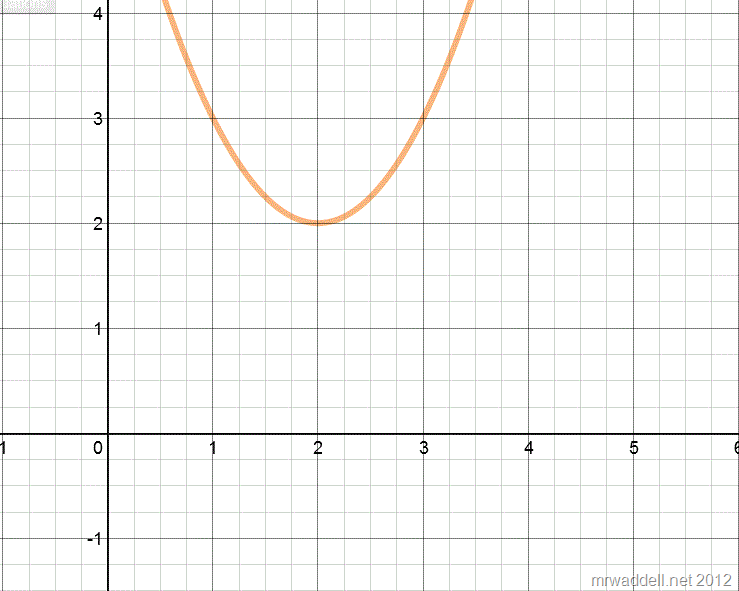
\[ y=x^2-4x+6 \]
Now they have to do the whole Quadratic formula to get the solution, and the solution has those i thingies in it, which makes them all confused and irritated until they wrap their heads around it. And why does it still have 2 solutions? It doesn’t touch at all!
But wait! We can play a game with this quadratic function. What if we reflect the parabola around the vertex in the downward direction? Then we end up with something that looks like this:
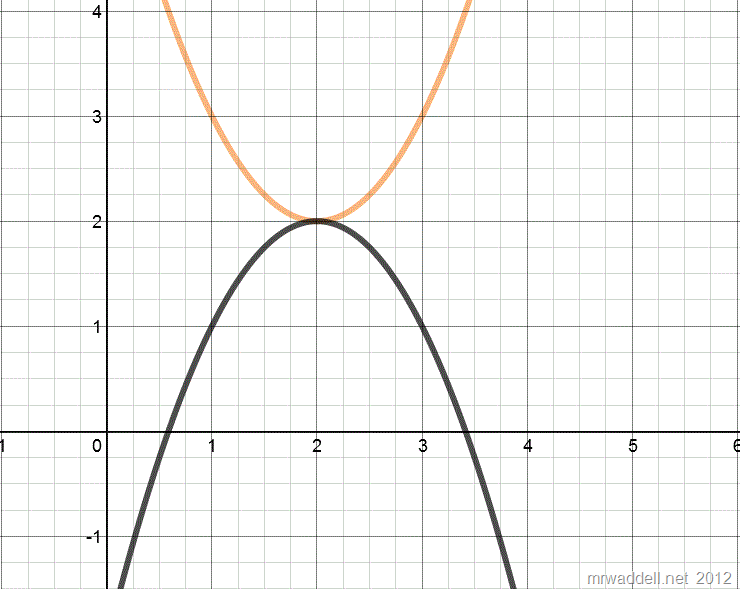
To do this reflection, we first have to complete the square on the original equation to get
\[ y = (x-2)^2 +2 \].
Now, with this equation, we can put a minus sign into the equation and get the reflection, \[ y = -(x-2)^2 + 2. \]
But hold on, see those 2 points where it crosses the X-axis? And see the Axis of Symmetry that goes through both equations? If we use those three points as definitions for a circle, we get the following graph and equation.
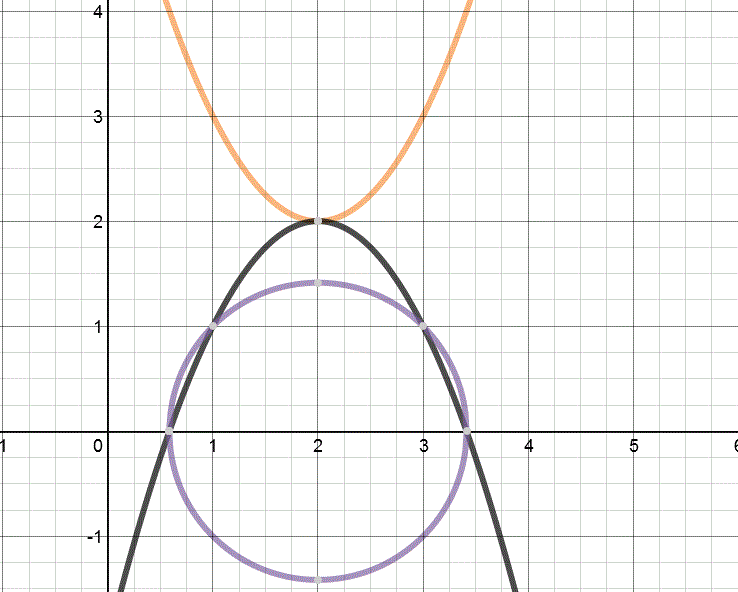
\[ (x-2)^2 + y^2 = 2 \]
Guess what the solution to the original quadratic equation is. If you guessed \[ 2 + i\sqrt{2} \quad \textrm{and} \quad 2 – i\sqrt2 \] then you are absolutely correct.
The real number part of the complex solution of a quadratic with two imaginary roots is the x value of the Axis of Symmetry. That is easy to see and understand. On to the more abstract.
If we rotate the circle out of the page 90 degrees (or, if we rotate the circle orthogonal to the page) we will now have the circle in the IMAGINARY plane! And the radius of the circle is sqrt(2), which we add and subtract to the center for the imaginary roots (and we multiply by i, because we are in the imaginary plane, not the real plane).
[If we want to get sloppy for a second, we could say that the reflected parabola shows us where those two roots are. BUT, this is sloppy, and useful only to help learners understand that there is a connection between the original parabola and the roots we calculate using the Quadratic Function. ]
Okay, mind blown. Why? How could I prove this is always true in general?
Aha! now comes into play the hours I spend on a motorcycle every summer. How could I PROVE that this will always work? I have the proof.
Okay, on to the proof! (this was originally 2 different posts, but I am combining them since I can. And since I am rebuilding them anyway.)
The Goal:
To prove that in a general case, the circle that is created by reflecting a parabola with imaginary roots (the orange one above) about its vertex (the black one above) will have as its radius the value of the imaginary roots of the original.
We will begin with:
\[ y=ax^2-bx+c \tag{1}\]
as our initial equation, with one requirement that the discriminate is negative;
\[ b^2 -4ac < 0 \tag{2}\]
This will ensure that our initial quadratic equation has imaginary roots and the parabola exists above the x axis as shown.
Now, we need to reflect this equation around the vertex, but just adding a negative sign in front of the “a” will not do it. If we add that sign in and make it “-a” it will reflect around the x-axis, not the vertex. Therefore, we are going to need to complete the square, get the original equation in vertex form and then introduce the minus sign to reflect.
Given the equation
\[ y=ax^2-bx+c \tag{3}\]
First, set the y=0, and divide all terms by “a”:
\[ 0= x^2 - \frac{b}{a} x + \frac{c}{a} \tag{4}\]
This gives us a first coefficient of 1, which makes
Completing the square much, much easier. Next, we will complete the square by using they standard method, and square of the term. The square is added and subtracted from the same side of the equation. (It could be added to both sides, that is a personal preference.)
\[ 0 = x^2 + \frac{b}{a} + \left(\frac{b}{2a} \right)^2 - \left(\frac{b}{2a} \right)^2 + \frac{c}{a} \tag{5}\]
From here, we construct the perfect square trinomial with the extra two terms
\[ 0 = \left(x + \frac{b}{2a} \right)^2 - \left(\frac{b}{2a} \right)^2 + \frac{c}{a} \tag{6}\]
And we now have the equation in its ‘vertex’ form, where the vertex is (h,k), and the h value is also the value of the axis of symmetry. It is also the x value of the center of the circle we are looking for, and since it is on the x axis, the center is:
\[ \left(-\frac{b}{2a} , 0 \right) \]
We will need this later.
The reflected parabola is easy to find from equation 6, the vertex form. All we need to do is reflect the equation around the vertex.
\[ 0 = -\left(x + \frac{b}{2a}\right)^2 - \left(\frac{b}{2a} \right)^2 + \frac{c}{a} \tag{7}\]
Add & Subtract the constant terms from both sides, and multiply by -1:
\[ -\left(\frac{b}{2a} \right)^2 + \frac{c}{a} = \left(x + \frac{b}{2a} \right)^2 \tag{8}\]
Take the square root of both sides:
\[ \pm \sqrt{-(\frac{b}{2a})^2 + \frac{c}{a}} = x + \frac{b}{2a} \tag{9}\]
Finally subtract the constant term from both sides:
\[ - \frac{b}{2a} \pm \sqrt{-\left(\frac{b}{2a}\right)^2 + \frac{c}{a}} = x \tag{10}\]
Notice that we have essentially derived a version of the quadratic formula. It doesn’t look exactly like the standard version we all memorize, but it is the same, with one important difference. There is a sign change to the terms inside the radical sign! That will be very important.
This formula gives us where the reflected parabola crosses the x-axis, so we now have 2 points on the circle, the plus and minus, and the center of the circle.
The final step of the proof is to show that the radius of the circle, or to put it in another way, the distance from the center of the circle to one of the roots of the reflected parabola, is identical to the imaginary part of the solution / roots of the non-inverted parabola. So, onward to the distance formula.
We need to find the distance from
\[ \left( -\frac{b}{2a} , 0 \right) \quad \textrm{to} \quad \left(- \frac{b}{2a} \pm \sqrt{-\left(\frac{b}{2a}\right)^2 + \frac{c}{a}},0 \right) \tag{11}\]
Distance formula comes in handy here:
\[ D=\sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} \tag{12}\]
Insert the values for x and y from our two points (thankfully the y’s are both zero), and using only the + value from the plus/minus:
\[ D= \sqrt{ \left(\ -\frac{b}{2a} - \left(- \frac{b}{2a} + \sqrt{-(\frac{b}{2a})^2 + \frac{c}{a}} \right) \right)^2 + (0-0)^2} \tag{13}\]
This appears ugly, but the first two terms are zero, the third term is squared, leaving us with:
\[ D = \sqrt{- \left( \frac{b}{2a} \right)^2 + \frac{c}{a}} \tag{14}\]
This must be positive because distances are always positive, so we know that this value is positive as well, so we do not have an imaginary number.
[And yes, I am cheating. I am leaving it to the reader to show that the way it is written above in the last step as the distance and the regular discriminant are essentially equivalent.]
At this point, with some additional algebra, we can see the typical “right” part of the quadratic formula,
\[ \frac {\sqrt{b^2 -4ac}}{2a} \tag{15}\]
We are only missing the “left” part, the location of the center of the circle:
\[ \frac{-b}{2a} \]
assembling the distance from the center, on either side of the center, of the circle, we get the both distances:
\[ \frac{-b}{2a} \pm \frac {\sqrt{b^2 -4ac}}{2a} \tag{16}\]
And voila! We have proven that the circle represents the roots of the quadratic! And along the way, have also derived the quadratic formula.
Yay!
And of course, I did not discover this, nor did I come up with this on my own. There was that website that gave me the initial idea, and there are other sources that explain this better.
For example, Francis Su does a clearer and better explanation on his site. This resembles what I described in 2012, but it was not this site or image. Clearly the image and idea has been around a long time. I spent hours trying to figure out how to prove this idea, and Francis gives a better method for proving it right there at the bottom!
There is a great video introducing complex numbers, found here.
And this amazing link pushes the idea into 3 dimensions. Love this!
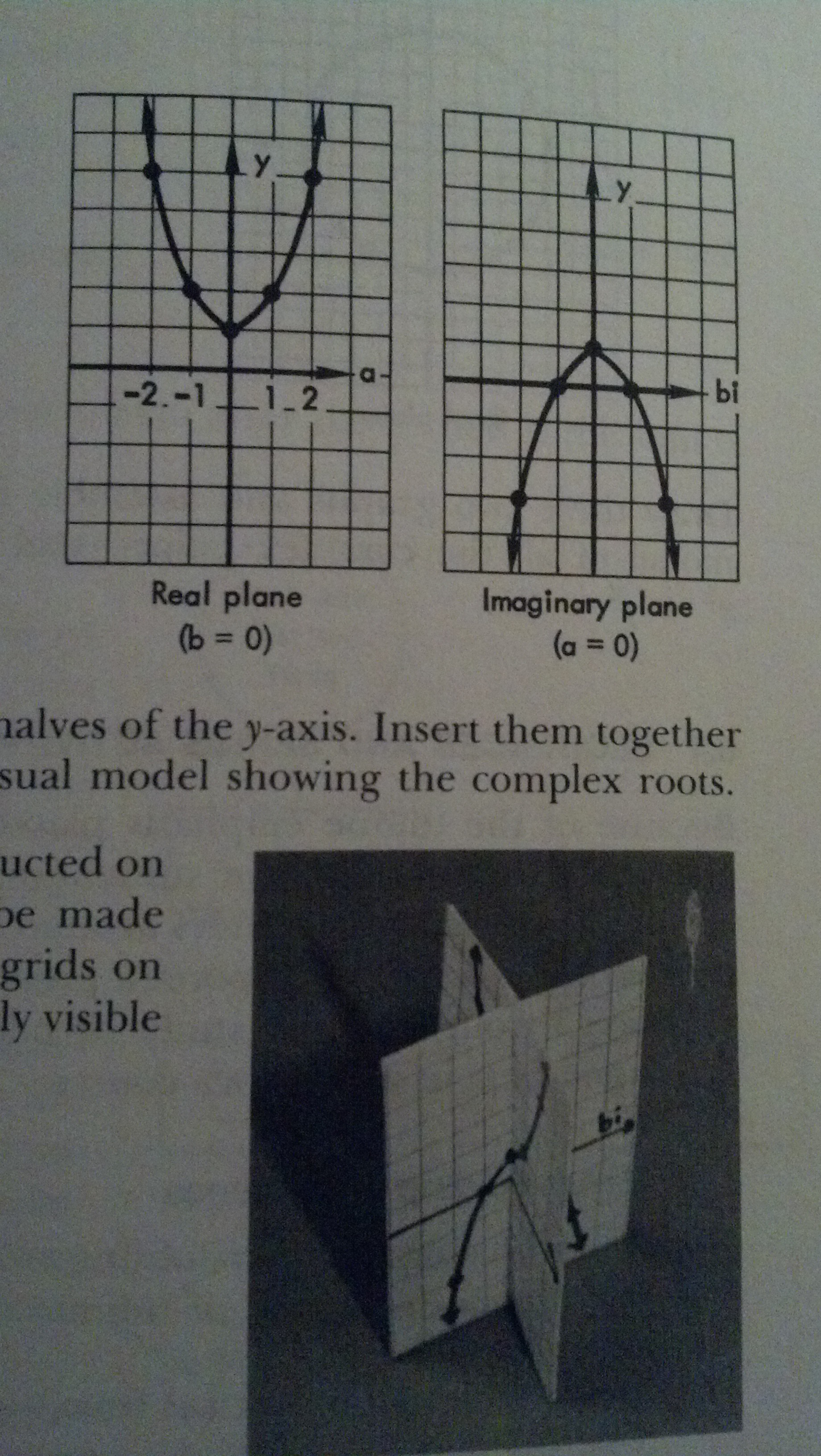
Also, from Teaching Mathematics, 2nd edition by m. Sobel and E. Maletsky. This image gives a very clear, understandable way to connect this for learners. This book is now in the 3rd ed, and fairly inexpensive to purchase.
Also, in my recreating this post, I had the advantage of using RStudio and Quarto, which means I was able to write this in LaTeX. The first time, in 2012, I wrote all the equations in Word’s editor, and pasted them as images. So much easier just to write in LaTeX.