Quadratics - starting the exploration
The main post where all my quadratic posts are listed can be found here.
I want to start the exploration here with an introduction that maybe not every teacher or math person has thought about. We jump to quadratics, and sometimes don’t think about how we build a quadratic function from simpler, more basic functions. For example, look at the image:
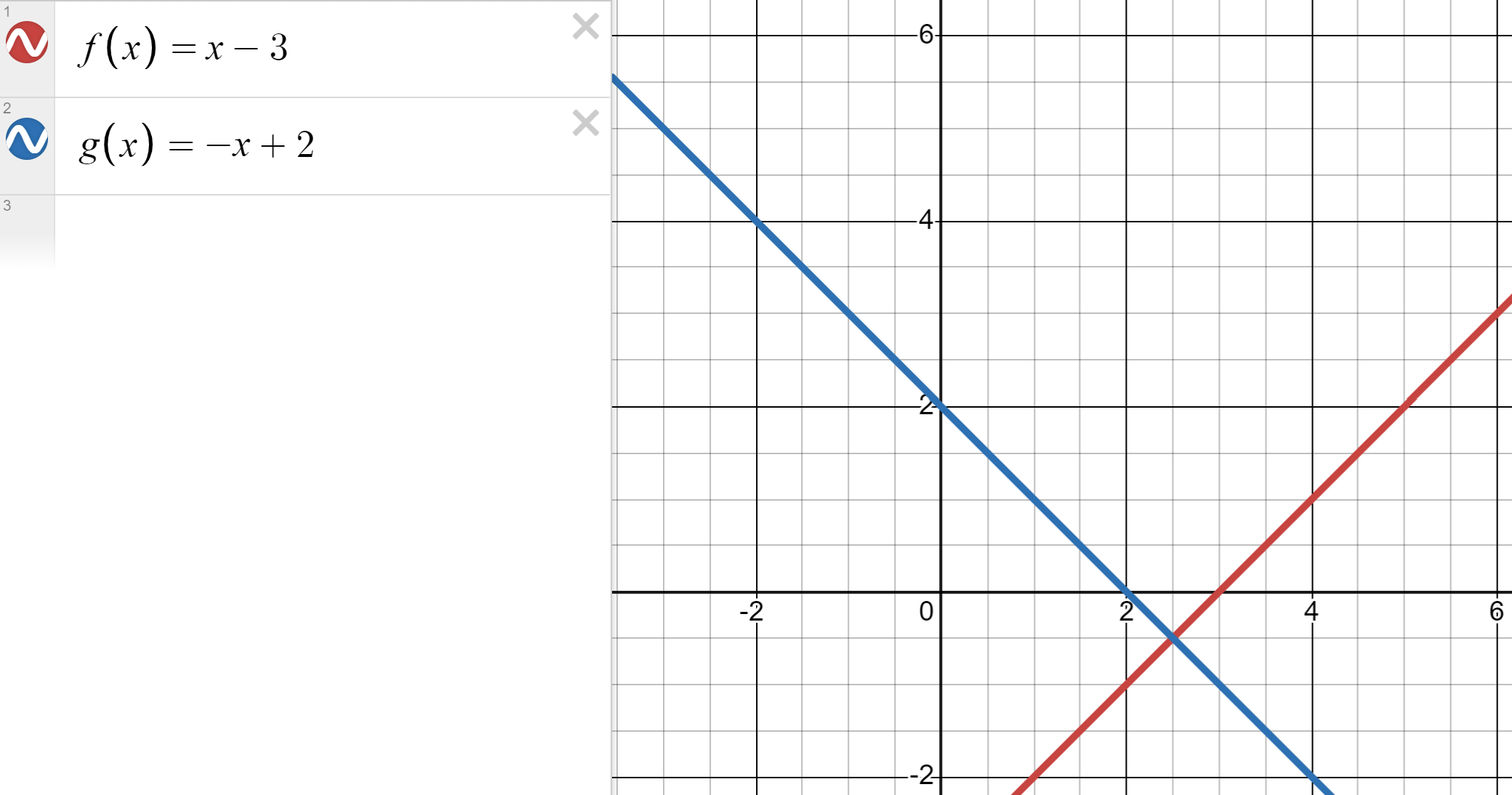
I intentionally wrote the two lines in function notation. We have one line with a negative slope and x-intercept of (2,0) and another line with a positive slope and an x-intercept of (3,0). They have an intercept with each other at (2.5,-0.5).
But look what happens when we multiply the two functions.
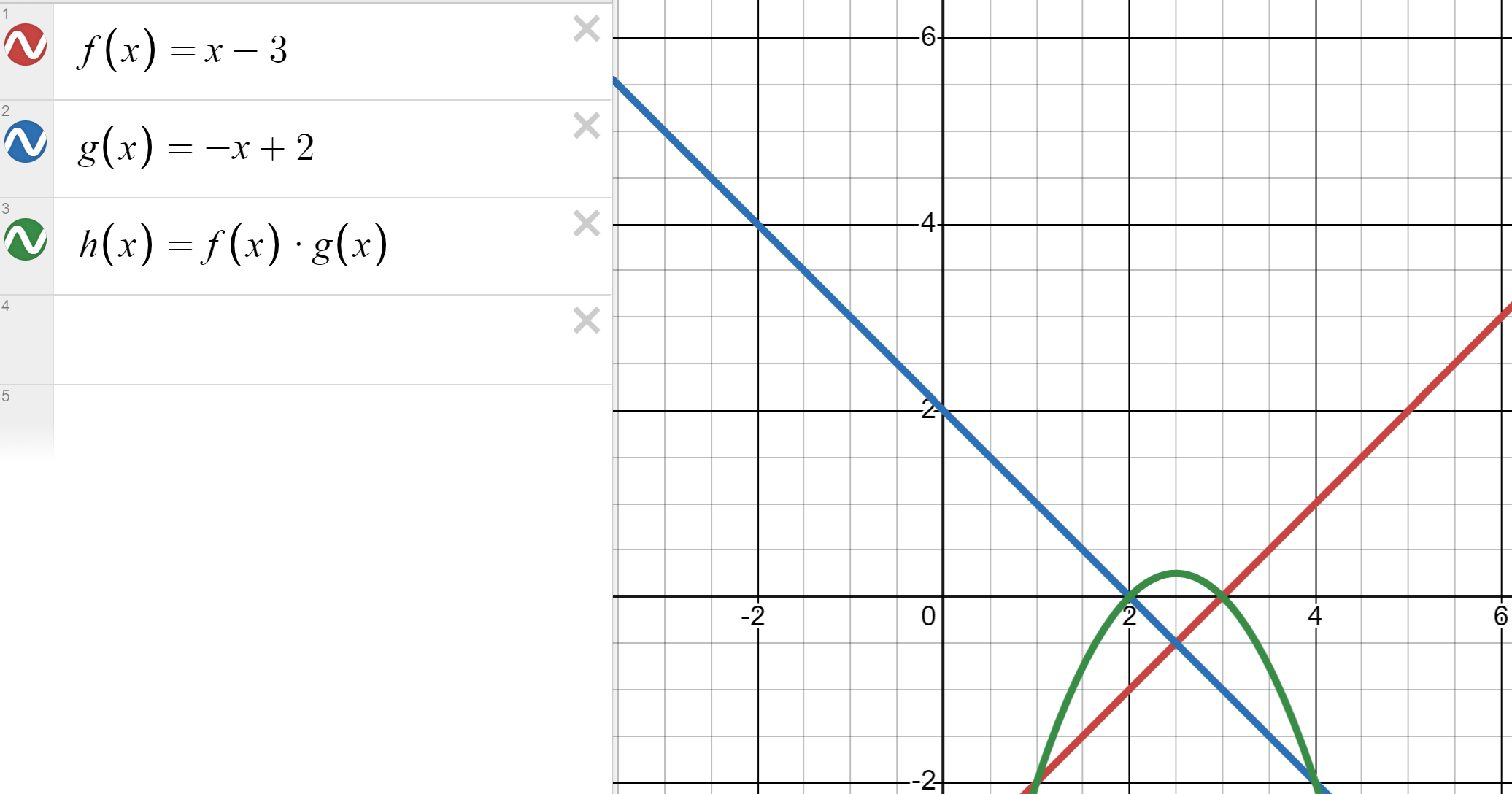
We get the quadratic! In fact, we get the intercept form of the quadratic function! And, since the two lines intersect, we get the vertex as the x value of the line intersection, and the square of the y value, or (2.5,+0.25).
Of course, this doesn’t work if the lines are parallel or have different slopes. Then the vertex of the parabola is the average of the x-intercepts of the lines, and then the values multiplied.
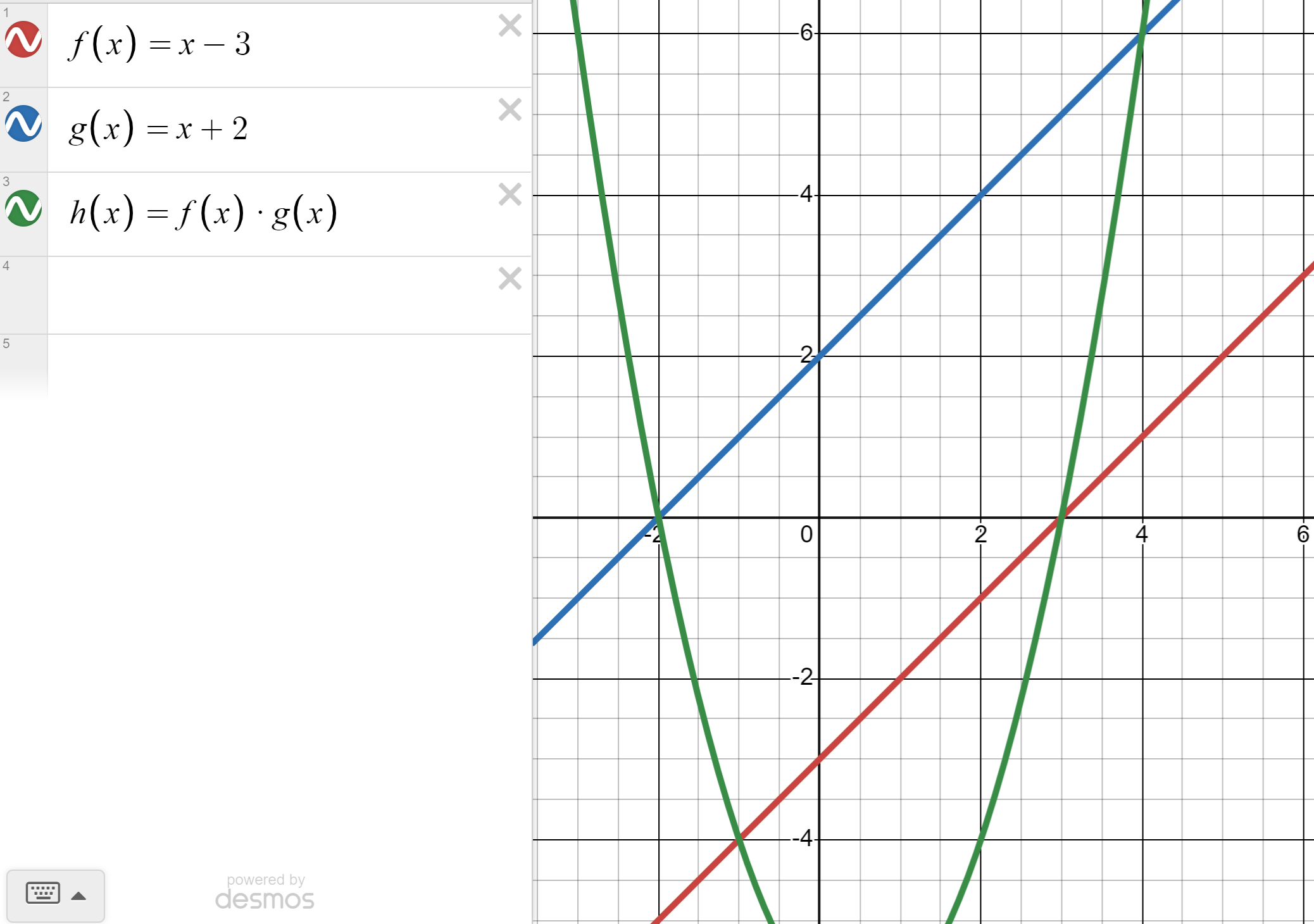
In this case, the average is 0.5, so the y value of the vertex is found at f(0.5)*g(0.5), so the vertex is (0.5, -6.25).
Yeah, yeah, yeah, we have other tools to find these same values, but the lines literally give us the answers! A quadratic function is constructed from two lines multiplied. If we want to connect lines to the rest of the algebra curriculum, start here.
I also want to take a moment to reinforce some important language. I have tried to be careful in my explanations above, and use the appropriate language of roots, zeros, solutions, and intercepts. The language often gets muddled, and I know some teachers have even called these items “ZIRaS” which stands for “Zeros, Intercepts, Roots and Solutions” because they “mean the same thing.”
I want to argue they don’t. Why would we have four different words for the same thing? As math people, we would not. If we have four words, it is because they four things mean something different.
Sarah, at the blog “Math = Love” has a great post on this. She even has posters you can download.
The following is the correct usage of the terms:
Expressions have Roots: (x-3)(x+2)
Equations have Solutions: (x-3)(x+2) = 0
Functions have Zeros: f(x) = (x-3)(x+2)
Graphs have x-intercepts: see the graph above.
But wait, you say. The answers to each of the four different things above are the same values. Not quite, I say. The x-intercepts are points. (3,0) and (-2,0). That matters. A lot. We get them by looking at the graph, and seeing where the parabola crosses the x axis.We get that from the graph of the parabola (the actual shape of the quadratic function).
The zeros of the function are numbers that when substituted into the function produce a zero output, ie.where f(x)=0. In this case, the two values are x=3 and x=2. If we are not careful, we could assume that we just described two vertical lines, but we did not. We described two values to substitute into a function.
The solution is the values we get by using the zero product property, after setting the equation equal to zero. We set each of the two products equal to zero and solve, (x-3)=0 and (x+2)=0, which results in two answers, x=3, and x=-2. Again, if these were on a graph, they would be vertical lines. We are not graphing.
Finally, the roots. This one is more abstract to explain, because the roots are simply (x+2)(x-3). The roots are the factored form of the quadratic expression, and it isn’t equal to anything, so we can’t set it equal to zero. If it was equaling zero, it would be an equation!
This post sets the stage for the rest. I am going to be careful in language, but also push some boundaries into different aspects of quadratics. Let me know on Bluesky or Mastodon what you think. I haven’t figured out how to incorporate comments here yet.